오늘은 Recursion에 대해서 공부해보겠습니다.
Recursion은 반복, 재귀로 많이 알려진 알고리즘인데요
자기 자신을 다시 호출하는 함수(메서드)를 의미합니다
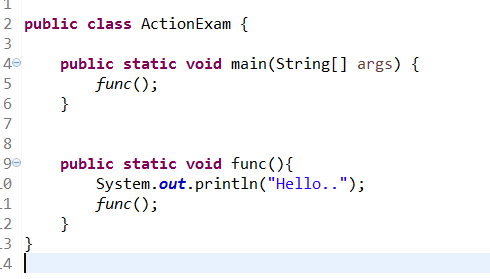
기본구조는 위 사진입니다.
하지만 위 사진의 코드는 치명적인 단점을 가지고 있습니다.
바로 코드가 무한루프에 빠진다는 점이죠!
종료조건(Base case)와 반복조건(recursion case)로 안 나눠져있기 때문입니다.
정확히 따지면 종료조건이 없어서 무한루프에 빠진다고 할 수 있습니다.
다시 한번 코드를 짜봅시다.

이렇게 짜면 Hello...가 4번만 출력되고 종료가 됩니다.!
그래서 재귀는 적어도 하나의 종료조건이 있어야 한다는 조건이 있어야합니다!
다음 예제를 살펴보도록 하겠습니다.
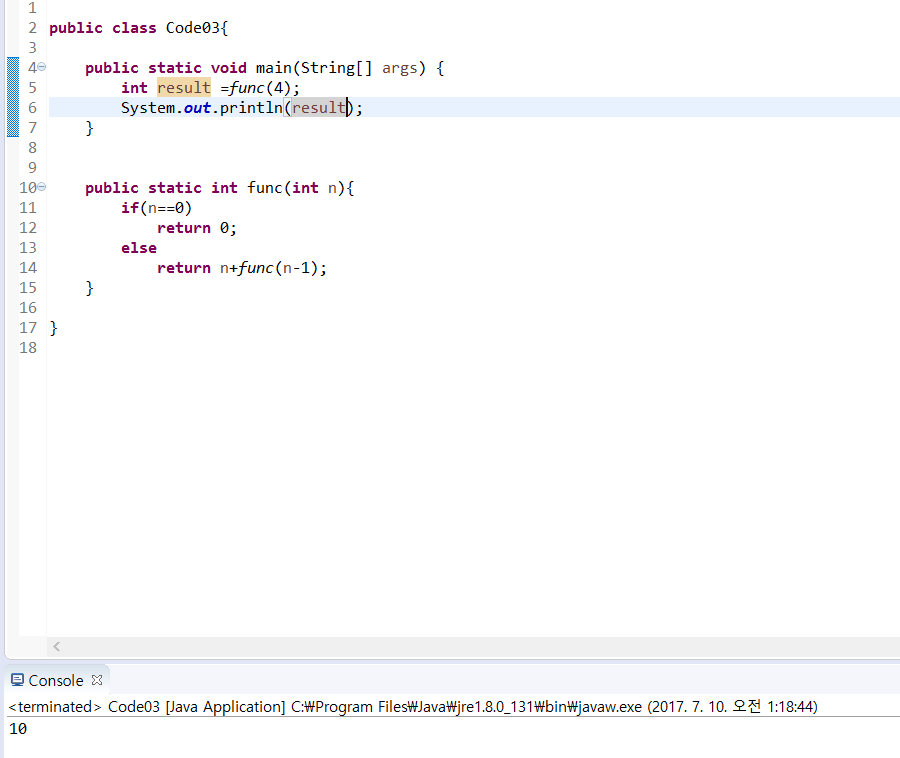
위 코드를 실행하면 10이 출력되는걸 볼 수가 있습니다
왜그럴까요? 이제 알아보겠습니다.

위 에 그림에서 맨 처음에 n에 4가 들어가면 n이 0이 아니니 4+func(3)이 return 됩니다
그 전에 func(3)이 호출되어서 같은 방법으로 3+func(2)이 return됩니다
같은방법으로 1+func(0)까지 쭉 내려가서 func(0)일떄 0이 return되고 함수가 종료가 되니 거꾸로 쭈욱 더해가서 10이 되는것입니다.

결과적으로 위의 코드의 Recursion의 해석은 0에서 n까지의 합을 의미합니다
이제 합을 구했으니 곱을 구하는 즉 Factorial을 구하는 코드를 알아봅시다!
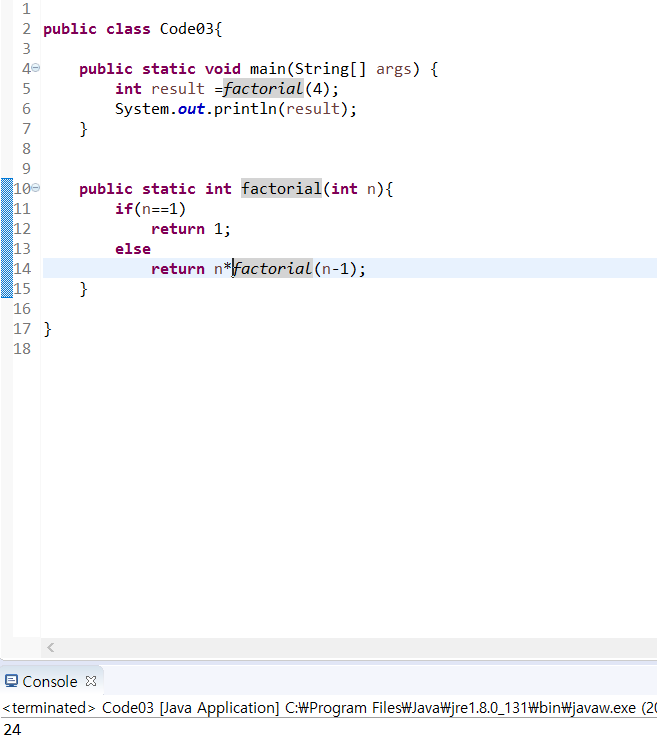
눈치가 빠르신 분들은 이제 눈치채셨겠죠? 1부터 4까지의 곱을 구하는 코드랍니다
이제 한번 분석해볼까요?

더하기와 동일하게 factorial(0)이 될떄 1이 return이 되고 그 위로 쭈욱 곱해주시면 됩니다.
왜 더하기는 0인데 곱하기는 1이냐? 그건 덧셈의 항등원이 0이고 곱셈의 항등원이 1이기 때문입니다.
기초적인 예제를 지나 조금 생각 할 만한 예제인 최대 공약수 구하기 알고리즘을 재귀로 구현해보겠습다

a>=b인 두 양의 정수 a,b에대해서 a이 b의 배수이면 gcd(a,b)=b
그렇지 않으면 gcd(m,n)=gcd(m,m%n)이다 라는
알고리즘을 가지고 구현한 최대공약수 구하는 알고리즘입니다
오늘은 여기까지 포스팅하겠습니다
출저 : My 노트북 Eclipse
유튜브 강좌 :https://www.youtube.com/watch?v=ln7AfppN7mY&list=PL52K_8WQO5oUuH06MLOrah4h05TZ4n38l&index=1



